| melky | 15.11.2012 17:34 |
Цитата:
|
Сообщение от cyber
(Сообщение 216062)
melky, 0,0 находиться по центру.
|
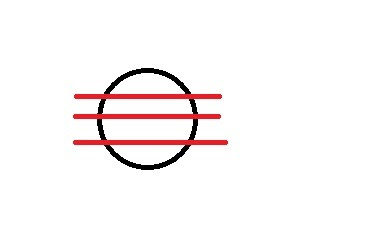
надеюсь, картинка прояснит :

немного поменял твой код - рисуется окружность в (0;0)
Цитата:
|
Сообщение от cyber
(Сообщение 216064)
melky,
<!DOCTYPE HTML>
<html>
<head>
<style>
canvas {
border:1px solid black;
}
</style>
</head>
<body>
<canvas width="500" height="500" id="canvas"></canvas>
<script>
var canva = document.getElementById("canvas");
var ctx = canva.getContext("2d");
ctx.width = 500;
ctx.height = 500;
var radius = 40;
ctx.arc(0,0,radius,0 , (Math.PI/180)* 360);
ctx.fill();
ctx.beginPath();
</script>
</body>
</html>
|
Цитата:
|
Сообщение от cyber
(Сообщение 216064)
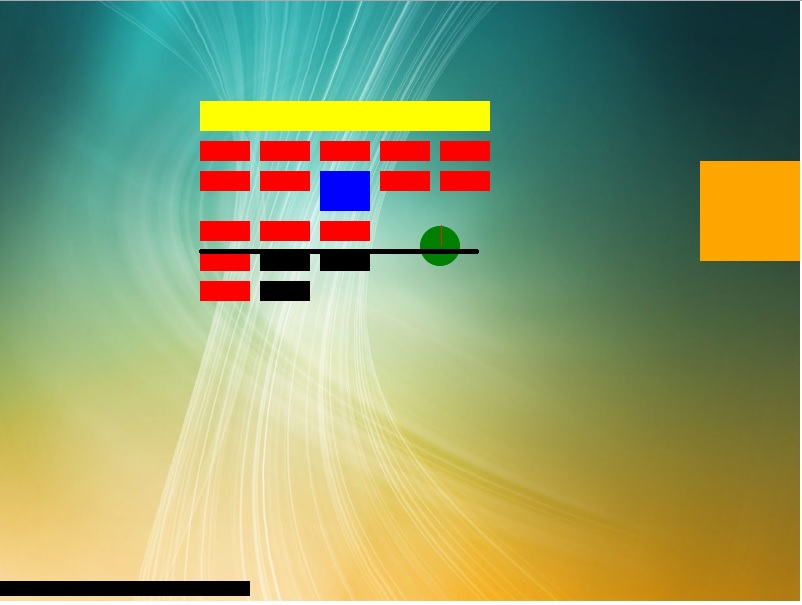
если бы он был с лева в верху то мне можно было смело идти переписывать 70% логики моего арканоида)
|
Цитата:
|
Сообщение от Дзен-трансгуманист
(Сообщение 216072)
Ага, если только translate не применял. ;)
|